|
|
Výsledky státní maturity z matematiky podzim 2016
Jak se říká někdo září, někdo v září, ale zazářili jste v září v maturitě z matematiky? Jestli pro vás byl první školní den tím definitivně posledním na střední škole, vám možná napoví naše neoficiální výsledky, které vám všem, co jste maturovali na pozdim 2016, přináší naše vzdělávací centrum Pochopim.cz.
Maturuješ letos? Připravuj se s námi!
|
Bez záruky
|
 1. Počáteční cena akcie nejprve klesla o 20 % a pak tato nová cena vzrostla o 20 %. Výsledná cena akcie je 1296 Kč. Vypočtěte počáteční cenu akcie. 1. Počáteční cena akcie nejprve klesla o 20 % a pak tato nová cena vzrostla o 20 %. Výsledná cena akcie je 1296 Kč. Vypočtěte počáteční cenu akcie.

 2. Zjednodušte 2. Zjednodušte

 3. Je dán výraz: 3. Je dán výraz:

 4. Pro a z R\ {-2;1;2} zjednodušte: 4. Pro a z R\ {-2;1;2} zjednodušte:
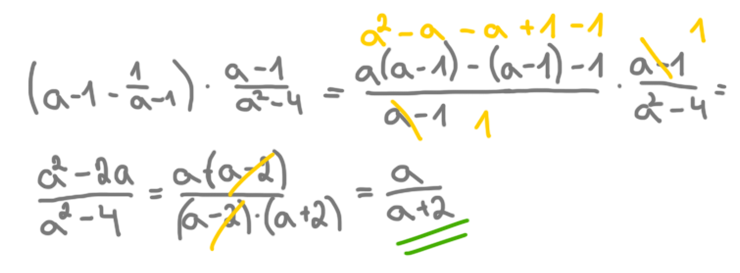
 5. V oboru R řešte: 5. V oboru R řešte:

 6. Je dána funkce f s předpisem y = x2 s definičním oborem Df=<-2;3>. Zapište obor hodnot funkce. 6. Je dána funkce f s předpisem y = x2 s definičním oborem Df=<-2;3>. Zapište obor hodnot funkce.

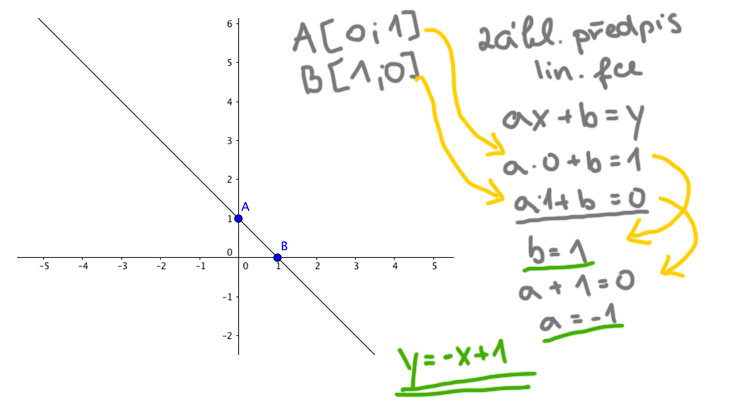
 7. Grafem funkce g je přímka. Zapište předpis funkce g. 7. Grafem funkce g je přímka. Zapište předpis funkce g.
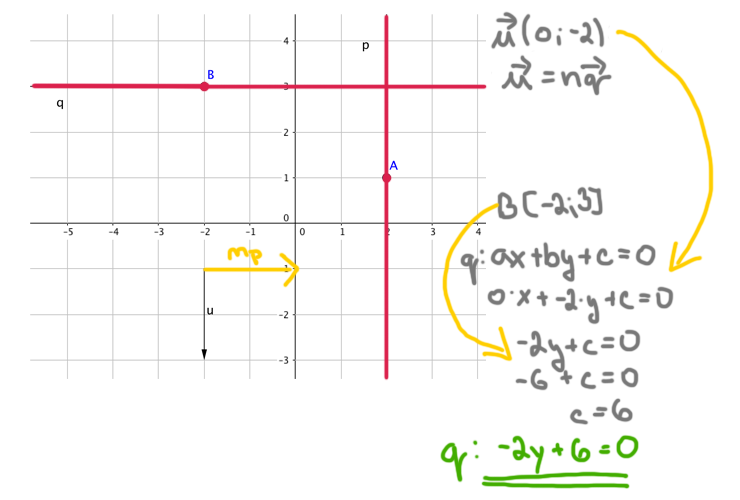
 8. Přímka p je určena bodem A a směrovým vektorem u. Přímka q prochází bodem B a je kolmá k přímce p. 8. Přímka p je určena bodem A a směrovým vektorem u. Přímka q prochází bodem B a je kolmá k přímce p.
 9.Ze čtvrtletní práce získalo 22 žáků 3. B následující známky: 3, 4, 2, 5, 4, 3, 4, 2, 1, 4, 3, 4, 5, 2, 4, 3, 2, 4, 5, 1, 3, 4. Určete medián (9.1) a modus (9.2) známek ze čtvrtletní práce. 9.Ze čtvrtletní práce získalo 22 žáků 3. B následující známky: 3, 4, 2, 5, 4, 3, 4, 2, 1, 4, 3, 4, 5, 2, 4, 3, 2, 4, 5, 1, 3, 4. Určete medián (9.1) a modus (9.2) známek ze čtvrtletní práce.

 10. Všechny vagóny nákladního vlaku jsou plně naloženy pískem, který přivezla malá a velká nákladní auta.
Malých aut bylo n (n je číslo sudé), velkých aut bylo o polovinu více než malých aut. Písek z malého auta naplní osminu vagónu a písek z velkého auta čtvrtinu vagónu. V závislosti na veličině n vyjádřete počet vagónů nákladního vlaku. Výraz zapište ve tvaru jednočlenu. 10. Všechny vagóny nákladního vlaku jsou plně naloženy pískem, který přivezla malá a velká nákladní auta.
Malých aut bylo n (n je číslo sudé), velkých aut bylo o polovinu více než malých aut. Písek z malého auta naplní osminu vagónu a písek z velkého auta čtvrtinu vagónu. V závislosti na veličině n vyjádřete počet vagónů nákladního vlaku. Výraz zapište ve tvaru jednočlenu.

 11. Trojciferné číslo má splňovat následující podmínky: V dekadickém zápise je na místě stovek sudá číslice, na místě desítek lichá číslice a na místě jednotek libovolná číslice, která nebyla použita na předchozích místech. (Vyhovují např. čísla 261, 610, 414.) Určete počet všech čísel, která splňují dané podmínky. 11. Trojciferné číslo má splňovat následující podmínky: V dekadickém zápise je na místě stovek sudá číslice, na místě desítek lichá číslice a na místě jednotek libovolná číslice, která nebyla použita na předchozích místech. (Vyhovují např. čísla 261, 610, 414.) Určete počet všech čísel, která splňují dané podmínky.

 12. Fiktivní obrazec je sestaven z podobných rovnoramenných trojúhelníků. Sousední trojúhelníky mají vždy jeden společný bod a jejich výšky na základnu leží na téže přímce.
Nejmenší trojúhelník má délku základny 2 cm a velikost výšky na základnu 1 cm. Každý další trojúhelník má uvedené rozměry dvakrát větší než předchozí trojúhelník. Obrazec obsahuje 6 trojúhelníků.
Vypočtěte v cm2 obsah největšího trojúhelníku. 12. Fiktivní obrazec je sestaven z podobných rovnoramenných trojúhelníků. Sousední trojúhelníky mají vždy jeden společný bod a jejich výšky na základnu leží na téže přímce.
Nejmenší trojúhelník má délku základny 2 cm a velikost výšky na základnu 1 cm. Každý další trojúhelník má uvedené rozměry dvakrát větší než předchozí trojúhelník. Obrazec obsahuje 6 trojúhelníků.
Vypočtěte v cm2 obsah největšího trojúhelníku.

 13. Zadání shodné s úlohou 12. Obrazec obsahuje 18 trojúhelníků.
Vypočtěte v cm výšku v celého obrazce. 13. Zadání shodné s úlohou 12. Obrazec obsahuje 18 trojúhelníků.
Vypočtěte v cm výšku v celého obrazce.

 14. V oboru R řešte: 14. V oboru R řešte:

 15. Sourozenci Adam, Bořek a Cyril spořili na společný dar.
Bořek uspořil 11 000 korun a Cyril třetinu aritmetického průměru úspor Adama a Bořka. Všichni tři chlapci dohromady uspořili třikrát více než samotný Adam.
Neznámý počet korun, které uspořil Adam, označte symbolem a. 15. Sourozenci Adam, Bořek a Cyril spořili na společný dar.
Bořek uspořil 11 000 korun a Cyril třetinu aritmetického průměru úspor Adama a Bořka. Všichni tři chlapci dohromady uspořili třikrát více než samotný Adam.
Neznámý počet korun, které uspořil Adam, označte symbolem a.

 16. Je dán bod P[3;-5]. O každé z následujících přímek ozhodněte, zda procházejí bodem P. 16. Je dán bod P[3;-5]. O každé z následujících přímek ozhodněte, zda procházejí bodem P.

 17. V rovině jsou dány body. Jaký obvod má čtverec ABCD? 17. V rovině jsou dány body. Jaký obvod má čtverec ABCD?

 18. Na číselné ose je obraz čísla 1. Které z následujících čísel má svůj obraz na číselné ose nejdále od obrazu čísla 1? 18. Na číselné ose je obraz čísla 1. Které z následujících čísel má svůj obraz na číselné ose nejdále od obrazu čísla 1?

 19. Šestiúhelník ABCDEF je složen z bílého lichoběžníku a dvou tmavých
rovnoramenných pravoúhlých trojúhelníků. Výška lichoběžníku je 4 cm, jedna jeho základna měří 6 cm a obsah lichoběžníku je 32 cm2. Jaký je obsah šestiúhelníku ABCDEF? 19. Šestiúhelník ABCDEF je složen z bílého lichoběžníku a dvou tmavých
rovnoramenných pravoúhlých trojúhelníků. Výška lichoběžníku je 4 cm, jedna jeho základna měří 6 cm a obsah lichoběžníku je 32 cm2. Jaký je obsah šestiúhelníku ABCDEF?

 20. Podél travnatého hřiště je natažena zahradní hadice. V libovolné části hadice řez vedený kolmo k ose hadice vytvoří mezikruží s vnitřním průměrem d = 26,3 mm. Jaké největší množství vody může obsahovat natažená hadice délky 50 m? Výsledek v litrech je zaokrouhlen na celé číslo. 20. Podél travnatého hřiště je natažena zahradní hadice. V libovolné části hadice řez vedený kolmo k ose hadice vytvoří mezikruží s vnitřním průměrem d = 26,3 mm. Jaké největší množství vody může obsahovat natažená hadice délky 50 m? Výsledek v litrech je zaokrouhlen na celé číslo.

 21. V rovnostranném válci je vytvořena dutina tvaru polokoule.
Poloměr podstavy válce i poloměr polokoule je r = 10 cm, výška válce je 2r. Jaký je povrch vytvořeného tělesa (tj. válce s dutinou)? 21. V rovnostranném válci je vytvořena dutina tvaru polokoule.
Poloměr podstavy válce i poloměr polokoule je r = 10 cm, výška válce je 2r. Jaký je povrch vytvořeného tělesa (tj. válce s dutinou)?

 22. Ve skupině jede 50 cyklistů. Celkem 10 z nich se provinilo konzumací alkoholických nápojů před jízdou.
Policejní hlídka vybere ze skupiny náhodně 5 cyklistů. Jaká je pravděpodobnost, že mezi vybranými cyklisty nebude žádný z 10 provinilců? Hodnota pravděpodobnosti je zaokrouhlena na setiny. 22. Ve skupině jede 50 cyklistů. Celkem 10 z nich se provinilo konzumací alkoholických nápojů před jízdou.
Policejní hlídka vybere ze skupiny náhodně 5 cyklistů. Jaká je pravděpodobnost, že mezi vybranými cyklisty nebude žádný z 10 provinilců? Hodnota pravděpodobnosti je zaokrouhlena na setiny.

 23. Po doplnění čísel do prázdných polí musí být zápis s uvedenými operacemi pravdivý. Doplní-li se do jednoho prázdného pole neznámá x, pak lze rovnicí dopočítat číslo, které neznámá x představuje. Která z následujících rovnic odpovídá naznačenému řešení na obrázku vpravo? 23. Po doplnění čísel do prázdných polí musí být zápis s uvedenými operacemi pravdivý. Doplní-li se do jednoho prázdného pole neznámá x, pak lze rovnicí dopočítat číslo, které neznámá x představuje. Která z následujících rovnic odpovídá naznačenému řešení na obrázku vpravo?

 24. Je dáno pět po sobě jdoucích členů aritmetické posloupnosti: 4, x, y, z,–8. Která hodnota vyjadřuje součet x + y + z? 24. Je dáno pět po sobě jdoucích členů aritmetické posloupnosti: 4, x, y, z,–8. Která hodnota vyjadřuje součet x + y + z?

 25. Přiřaďte ke každé rovnici její řešení v oboru R. 25. Přiřaďte ke každé rovnici její řešení v oboru R.

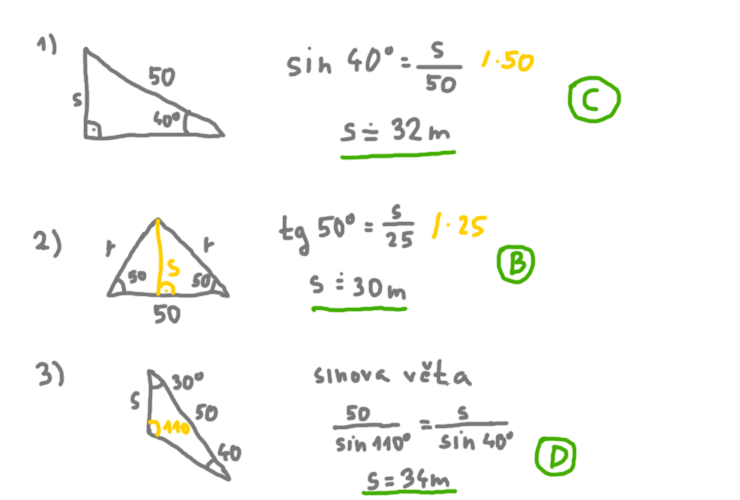
 26. V každé zobrazené situaci je šířka řeky označena symbolem s a vzdálenost AB je 50 m. Přiřaďte ke každé situaci odpovídající šířku řeky s. 26. V každé zobrazené situaci je šířka řeky označena symbolem s a vzdálenost AB je 50 m. Přiřaďte ke každé situaci odpovídající šířku řeky s.
|



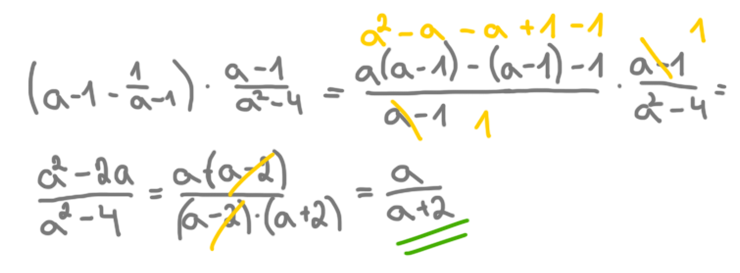
























 1. Počáteční cena akcie nejprve klesla o 20 % a pak tato nová cena vzrostla o 20 %. Výsledná cena akcie je 1296 Kč. Vypočtěte počáteční cenu akcie.
1. Počáteční cena akcie nejprve klesla o 20 % a pak tato nová cena vzrostla o 20 %. Výsledná cena akcie je 1296 Kč. Vypočtěte počáteční cenu akcie.












